
Peaks
Challenger
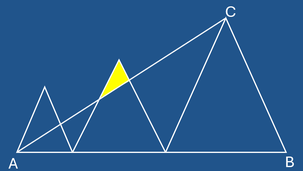
Given 3 similar isosceles triangles that touch each other at their bases, which all lie on the line AB (see figure). The bases are in the ratio 1:2:3. The area of the leftmost (smallest) triangle is 30. C is the vertex of the rightmost (largest) triangle.
The line AC cuts off a small triangle from the middle triangle. Calculate the area of that cut-off small triangle. Round your answer to the nearest whole number. Attention: the figure is not drawn to scale.
Mastermind

Given 4 similar isosceles triangles that touch each other at their bases, which all lie on the line AB (see figure). The bases are in the ratio 1:2:3:4. The area of the leftmost (smallest) triangle is 30. C is the vertex of the rightmost (largest) triangle.
The line AC cuts off small triangles from the two middle triangles. Calculate the total area of these two cut-off small triangles. Round your answer to the nearest whole number. Attention: the figure is not drawn to scale.