
Triangular Quadrangles
Given a triangle ABC. On AC are points D and E such that |AD|=|DE|=|CE|. On BC are points F and G such that |BF|=|FG|=|CG|. The lines AF, AG, BD and BE divide ABC into 5 triangles and 4 quadrangles. The area of triangle ABC is 420.
Challenger
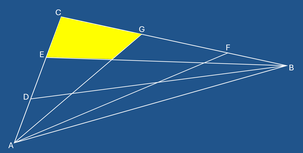
Determine the area of the upper quadrangle that has point C as one of its vertices. Round your answer to the nearest whole number. If the area is dependent on the shape of the triangle, submit 0 as your answer. Attention: the figure is not drawn to scale.
Mastermind
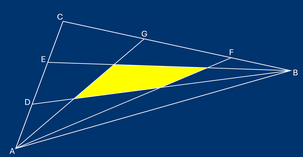
Determine the area of the central quadrangle. Round your answer to the nearest whole number. If the area is dependent on the shape of the triangle, submit 0 as your answer. Attention: the figure is not drawn to scale.